Rumus Getaran Beban Pada Ayunan Sederhana

193 views 1 Februari 1, 2023 editor

Pengertian

Getaran merupakan suatu peristiwa gerak bolak balik secara teratur suatu benda melalui satu titik seimbang, atau secara umum disebut sebagai gerak bolak-balik yang terdapat di sekitar kesetimbangan. Ayunan sederhana adalah suatu sistem yang terdiri dari sebuah massa titik yang digantung dengan tali tanpa massa dan tidak dapat mulur.jika ayunan ini ditarik ke samping dari posisi setimbang, dan kemudian dilepaskan,maka massa m akan berayun dalam bidang vertikal ke bawah pengaruh gravitasi .Gerak ini adalah gerak osilasi dan periodik. 

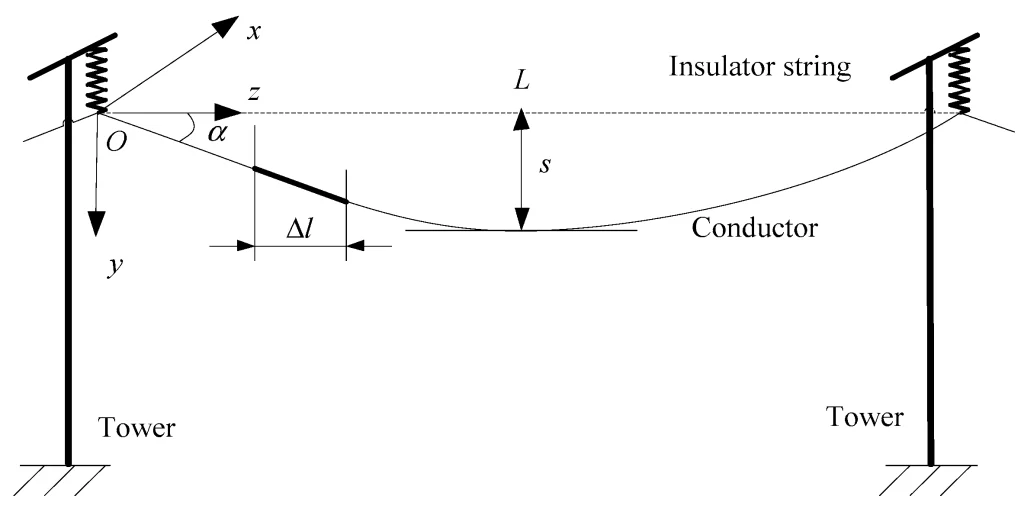
Rumus

  • Gaya Pemulih
\[F = -m \cdot g \cdot sin \ θ\]
  • Periode Ayunan
\[T = 2π \sqrt \frac{L}{g}\]
  • Frekuensi Ayunan
\[f = \frac{1}{2π} \sqrt \frac{g}{L}\]
  • Percepatan Ayunan
\[a = -g \cdot \frac{s}{L}\]

Keterangan :
T = periode (s)
f  =frekuensi (Hz)
m = massa (kg)
L = Panjang Tali (m)
g = Percepatan Gravitasi (m/s2)
s = simpangan (m)

Contoh

Sebuah ayunan bandul yang panjang talinya 200 cm dengan massa 120 g jika gravitasi 10 m/s2, Berapakah frekuensi dan periode ayunan bandul tersebut ?

  • Frekuensi
\[f = \frac{1}{2π} \sqrt \frac{g}{L}\] \[f = \frac{1}{2π} \sqrt \frac{10}{0,2}\] \[f = \frac{1}{2π} \cdot 7,07\] \[f = 3,53π \]
  • Periode
\[T = 2π \sqrt \frac{L}{g}\] \[T = 2π \sqrt \frac{0,2}{10}\] \[T = 2π \sqrt 0,02\] \[T = 2π \cdot 0,14\] \[T = 0,28π \]

Apakah informasi ini sudah membantu?

 
Rumus Terkait

Belum menemukan rumus yang kamu cari? Kontak kami

  

  

Popular Search:Customization, Policy, Setup